| BinomialHeap Documentation |
Home
|
Back
|
Forward
|
||||||
|
|
|||||||||
1. Binomial trees and binomial heaps
2. Operations on binomial heaps
2.1 Creating a new
binomial heap
2.3 Uniting two binomial
heaps
2.4 Inserting a node
2.5 Extracting the node with the minimum
key
2.6 Decreasing a key
2.7 Deleting a key
The binomial tree Bk is an ordered tree defined recursively. As shown in Figure 1(a), the
binomial tree B0 consists of a single
node. The binomial tree Bk consists of two binomial trees Bk-1 that are linked together: the root of one is the
leftmost child of the root of the
other. Figure 1(b) shows the binomial trees B0 through B4. Some properties of binomial trees are given by
the following lemma.
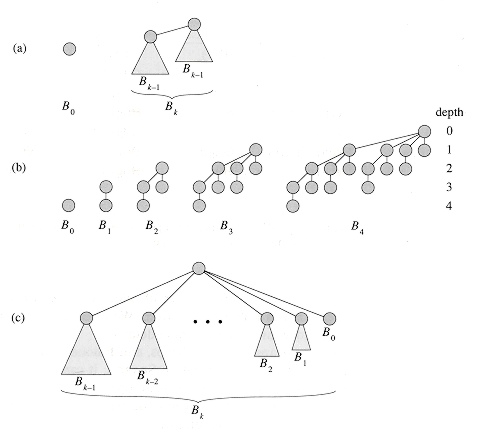
Lemma :
For the binomial tree
Bk,
1. there are 2k nodes,
2. the height of the tree is k,
3. there are exactly () nodes at depth i for i = 0, 1, . . . , k,
and
4. the root has degree k, which is
greater than that of any other node; moreover if the children of the root are
numbered from left to right by k – 1, k – 2, . . . , 0, child i is the root of
a subtree Bi.
A binomial heap H is a set of binomial trees that
satisfies the following binomial-heap properties.
1. Each
binomial tree in H is heap-ordered: the key of a node is greater than or equal
to the key of its parent.
2. There is
at most one binomial tree in H whose root has a given degree.
The first property tells
us that the root of a heap-ordered tree contains the smallest key in the tree.
The second property
implies that an n-node binomial heap H consists of at most lg(n) + 1 binomial
trees.
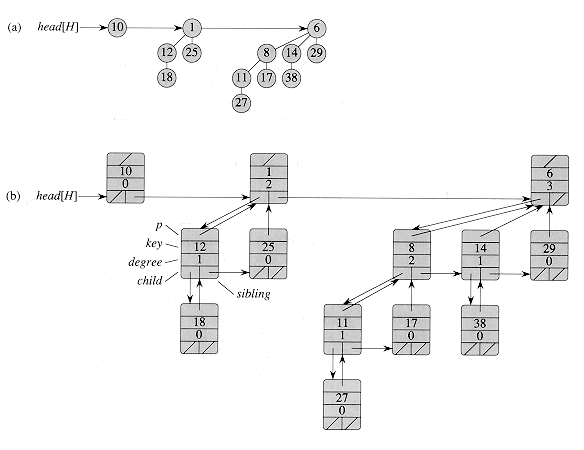
Figure 20.3 A binomial
heap H with n = 13 nodes. (a) The heap consists of binomial trees B0, B2, and
B3, which have 1, 4, and 8 nodes respectively, totaling n = 13 nodes. Since
each binomial tree is heap-ordered, the key of any node is no less than the key
of its parent. Also shown is the root list, which is a linked list of roots in
order of increasing degree. (b) A more detailed representation of binomial heap
H. Each binomial tree is stored in the left-child, right-sibling
representation, and each node stores its degree.
2.1 Creating a new binomial
heap
To make an empty binomial heap, the MAKE-BINOMIAL-HEAP
procedure simply allocates and returns an object H, where head[H] = NIL. The
running time is Q(1).
The procedure
BINOMIAL-HEAP-MINIMUM returns a pointer to the node with the minimum key in an
n-node binomial heap H. This implementation assumes that there are no keys with
value infinit.
BINOMIAL-HEAP-MINIMUM(H)
1 y ¬
NIL
2 x ¬
head[H]
3 min ¬+infinit
4 while x ¹ Ni IL
5 do if key[x] < min
6 then min ¬ key[x]
7 y ¬ x
8 x ¬ sibling[x]
9 return y
Since a binomial heap is heap-ordered, the minimum key must reside in
a root node. The BINOMIAL-HEAP-MINIMUM procedure checks all roots, which number
at most lg(n) + 1, saving the current minimum in min and a pointer to the
current minimum in y. When called on the binomial heap, BINOMIAL-HEAP-MINIMUM
returns a pointer to the node with key 1.
Because there are at most lg(n) + 1 roots to check, the running time
of BINOMIAL-HEAP-MINIMUM is O(lg n).
2.3 Uniting two binomial
heaps
The operation of uniting two
binomial heaps is used as a subroutine by most of the remaining operations. The
BINOMIAL-HEAP-UNION procedure repeatedly links binomial trees whose roots have
the same degree. The following procedure links the Bk–1 tree rooted at node y
to the Bk–1 tree rooted at node z; that is, it makes z the parent of y. Node z
thus becomes the root of a Bk tree.
BINOMIAL-LINK(y,z)
1 p[y] ¬ z
2 sibling[y] ¬ child[z]
3 child[z] ¬ y
4 degree[z] ¬ degree[z]+1
The
BINOMIAL-LINK procedure makes node y the new head of the linked list of node
z's children in O(1) time. It works because the left-child, right-sibling
representation of each binomial tree matches the ordering property of the tree:
in a Bk tree, the leftmost child of the root is the root of a Bk–1 tree.
The following procedure unites binomial heaps H1 and H2, returning the resulting heap. It destroys the representations of H1 and H2 in the process. Besides BINOMIAL-LINK, the procedure uses an auxiliary procedure BINOMIAL-HEAP-MERGE that merges the root lists of H1 and H2 into a single linked list that is sorted by degree into monotonically increasing order. The BINOMIAL-HEAP-MERGE procedure, whose pseudocode we leave as Exercise 20.2-2, is similar to the MERGE procedure.

The running time of BINOMIAL-HEAP-UNION is O(1g n), where n is the total number of nodes in binomial heaps H1 and H2. We can see this as follows. Let H1 contain n1 nodes and H2 contain n2 nodes, so that n = n1 + n2. Then, H1 contains at most 1g (n1) + 1 roots and H2 contains at most 1g (n2) + 1 roots, so H contains at most 1g (n1) + 1g(n2) + 2 = O(1g n) roots immediately after the call of BINOMIAL-HEAP-MERGE. The time to perform BINOMIAL-HEAP-MERGE is thus O(lg n). Each iteration of the while loop takes O(1) time, and there are at most 1g (n1) + 1g (n2) + 2 iterations because each iteration either advances the pointers one position down the root list of H or removes a root from the root list. The total time is thus O(lg n).
|
Made by Tiberiu
Petrica - UPB Computer Science 334CB
|